1 .目的
本文简要地阐述了BP人工神经网络的工作原理,主要面向没有神经网络知识的初学者。
2.生物体中的神经网络
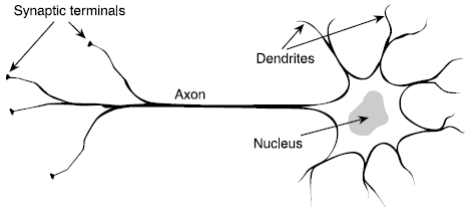
在生物体中,每个神经元都具有一个像绳索一样的线状物被称作轴突,它的作用是用来向其它神经元传递信号,除此了轴突,神经元上还有许多向各个方向分叉的较小的线状物,被称为树突。
神经元通过使用电化学过程交换信号。传入的信号在突触末端与树突连接处被接收。这些连接点被称为突触。
神经元将从突触传进的所有信号相加,如果总的信号强度超过了一个阈值,那么神经元被激发并且发送电子信号到它的轴突,要是总的信号强度没有超过神经元的阈值,那么神经元不会被激发。
3.人工神经网络
人工神经网络与生物神经网络的构建方式相同,都使用了很多的神经元。详见图2,它描绘了呈现一个人工神经元的一种方式,图中灰色圆圈中的W被称为权重(weights),它是浮点数类型的变量。 人工神经元的每个输入都有一个与之相关的权重,并且它的这些权重决定了神经网络的总体活动.
此刻假设所有的这些权重都被设置成小的随机值—比如说在-1.0和1.0之间。因为一个权重既可以是正值也可以是负值,它可以对与之相关的输入产生活跃的影响,也可以产生抑制的影响。当输入信号进入神经元时,这些输入乘以它们各自相关的权重。
人工神经元核心中的函数 – 激发函数 – 将所有这些新的被权重调整后的输入值相加以给出最终的激发值(同样是浮点数,可以是正值或负值)。
如果这个激发值是在一个确定的阈值以上,我们以数字1为例,那么神经元会输出一个信号并且这个信号的值为1.如果激发值小于1,那么人工神经元将会输出0.
这是人工神经元中最简单的激发函数之一,它被称为阶梯函数。
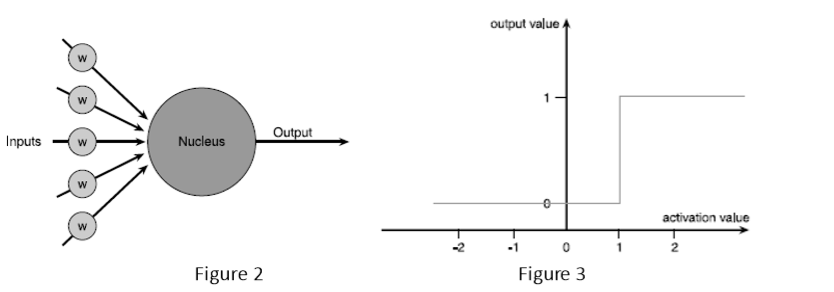
一个人工神经元可以有编号从1到n的任意数量的输入,其中n是输入的总数。
每个输入都可以用数学表示为: X1,X2,X3,X4….Xn,同样权重可以相似地表示为:W1,W2,W3,W4….Wn.
记住,激活值是所有输入乘以对应权重之和。它可以被表示为:
A = X1*W1+X2*W2+X3W3+X4*W4….+Xn*Wn,如图4所示。
如果激活值超过了神经元的阈值,那么神经元输出值为1;如果激活值小于神经元的阈值,那么神经元输出为0.
这与生物神经元激活与不激活相似。想像一个有五个输入的神经元,它所有的权重都被初始化随机的值((-1 < w < 1).
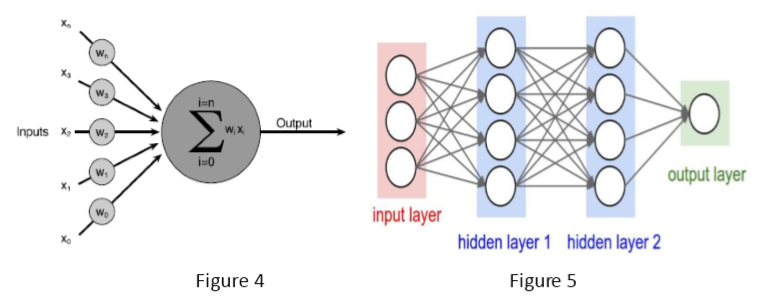
就像生物大脑中的一个神经元连接到另一个神经元那样,这些人工神经元以一定的规则连接在一起组成了神经网络。其中最广泛的应用就是将这些神经元分层的连接在一起,如图5所示,这种类型的人工神经网络被称为前向反馈网络。其中的每层神经元将它们的输出馈送到下一层,直到产生输出。每个输入都会被发送到隐藏层的每个神经元,然后隐藏层中每个神经元的输出都会被传送到下一层中的每个神经元。
在前向反馈网络中可以有任意数量的隐藏层,但是通常一个隐藏层足以应付你要解决的大部分问题。
事实上,每一神经层都可以有任意数量的神经元(具体的数量要取决于具体的问题)
4.BP误差反向传播算法
BP反向传播算法的工作原理如下:
首先创建具有一个或有更多隐藏层的神经网络,并且将所有的权重值都随机初始化,区间在-1.0到1.0之间。
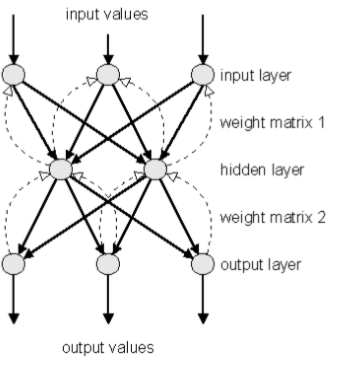
然后向神经网络呈现一种输入模式并注意它的输出。神经网络实际的输出值与期望的输出值之差成为误差值。这个误差值之后被用来决定如何调整输出层前一神经层的权重值,所以如果相同的输入模式再一次呈现,那么输出值将会更接近正确的值。
一旦调整了当前神经层的权重,就会对前一神经层重复相同的操作,直到达到第一个隐藏神经层为止,并且每个神经层的所有权重都已经被轻微地调整。
如果这个过程正确地被完成,那么下一次同一输入模式被呈现时,神经网络的输出将会离期望输出值更近一些。
然后用所有不同的输入模式多次重复整个过程,直到神经网络的误差值在当前要解决问题的可接受范围内。那么我们就说这个网络是经过训练的神经网络。
5.神经网络的训练
人工神经网络学习所需的训练集是一系列这样的向量,这组匹配的输入/输出模式用于训练网络如下:
1.初始化权重为小的随机值.
2.对每一种模式,重复步骤a到e:
a.呈现输入值到神经网络并且评估输出值o
b.计算实际输出值与期望输出值之间的误差
c. 计算隐藏层的误差值
d. 调整输出层的所有权重.
e. 调整隐藏层的所有权重.
3.重复步骤2直到所有误差之和在步骤b的可接受范围之内.
6.神经网络训练的公式总结
1.从输出层开始计算误差:
输出层神经元K的实际输出被表示为Ok,期望输出被表示为Tk.误差值被表示为Ek.
Ek = (Tk-Ok)* Ok(1- Ok)
2.计算隐藏层的误差:
隐藏层的神经元在j,它的误差值公式如下:
Ej = Oj*(1- Oj) *( E1 * Wj1 +E2 * Wj2 +E3 * Wj3 +…+ Ek * Wjk+…+ En * Wjn)
( n是输出层神经元的数量).
3.调整输出层的权重:
调整隐藏层神经元j与输出层神经元k之间的权重值的公式如下:
Wjk +=L* Ek*Oj
(L是一个小的正值,被称为学习率.学习率的值越大,权重值被调整的幅度就越大,为了得到最好的性能,这个值必须手动来调整)
4.调整隐藏层的权重:
调整隐藏层神经元j与输入层神经元i之间的权重公式如下:
Wij +=L* Ej*Oi
5.重复整个过程,直到所有训练模式的误差值降低到可接受的水平.